In order to understand the normalization method, certain rules of implication among FDs are given next.
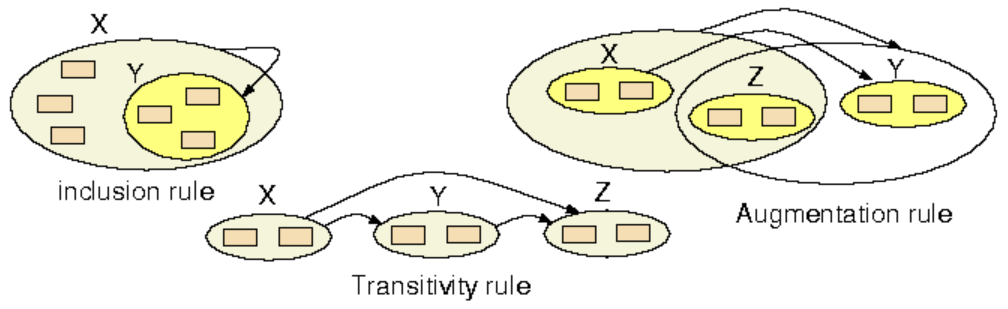
- Inclusion Rule
- Given a table
T, ifXandYare sets of attributes contained inHead(T), andY⊆X, thenX→Y. - Trivial Dependency
- A trivial dependency is an FD of the form
X→Ythat holds for any possible content of the tableTwhereX,Y⊆Head(T). - A Subset of Trivial Dependency
- Given a trivial dependency
X→Y, it must be the case thatY⊆X.
Armstrong’s Axioms
Given a table
T, and sets of attributes X,Y,Z⊆Head(T), then we have the following rules of implication:
- Inclusion Rule:
If
Y⊆X, thenX→Y. - Transitivity Rule:
If
X→YandY→Z, thenX→Z. - Augmentation Rule:
If
X→Y, thenXZ→YZ.
| There I was, in my birthday suit (nakedness), when the doorbell rang. |