Logical Implications Among FDs

---

In order to understand the normalization method, certain rules of implication among FDs are given next.

Inclusion Rule

Given a table T, if X and Y are sets of attributes contained in Head(T), and Y⊆X, then X→Y.

Trivial Dependency

A trivial dependency is an FD of the form X→Y that holds for any possible content of the table T where X,Y⊆Head(T).

A Subset of Trivial Dependency

Given a trivial dependency X→Y, it must be the case that Y⊆X.

The inclusion rule is one rule by which FDs can be generated that are guaranteed to hold for all possible tables. In turns out that from a small set of basic rules of implication, we can derive all others like Armstrong’s Axioms.

Armstrong’s Axioms
Given a table T, and sets of attributes X,Y,Z⊆Head(T), then we have the following rules of implication:

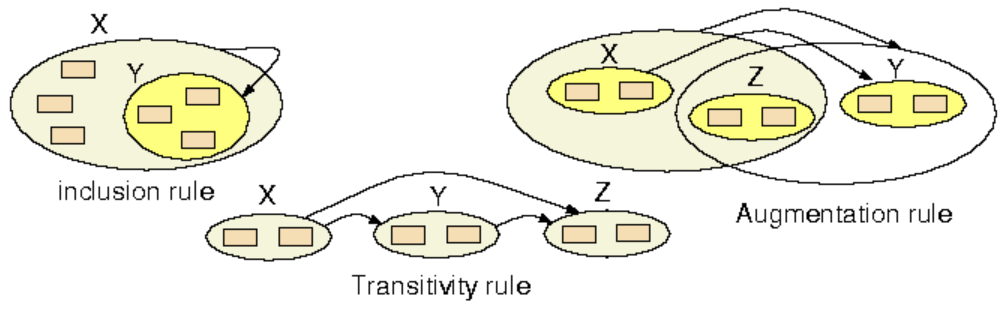
1. Inclusion Rule: If Y⊆X, then X→Y.


2. Transitivity Rule: If X→Y and Y→Z, then X→Z.


3. Augmentation Rule: If X→Y, then XZ→YZ.