Several options exist for modeling the behavior of a random web surfer after landing on a dangling node. One option replaces each dangling node row of
H by the same probability distribution vector, w, a vector with nonnegative elements that sum to 1.
The resulting matrix is S=H+dw, where
dis a column vector that identifies dangling nodes, meaningdi=1ifli=0anddi=0, otherwise; andw=(w1 w2 . . . wn)is a row vector withwj≥0for all1≤j≤nand Σwj=1wherej=1..n.
w is the uniform row vector, w=(1/n 1/n ... 1/n).
This amounts to adding artificial links from dangling nodes to all webpages.
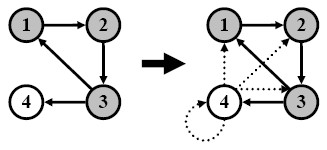
With w=(1/4 1/4 ... 1/4), the directed graph in the previous figure changes to the figure on the right.
|
|
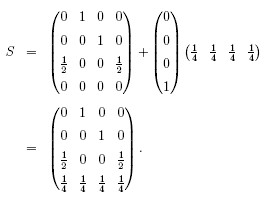
The new matrix
S=H+dw is given below.
Regardless of the option chosen to deal with dangling nodes, Google creates a new matrix S that models the tendency of random web surfers to leave a dangling node; however, the model is not yet complete.
Even when webpages have links to other webpages, a random web surfer might grow tired of continually selecting links and decide to move to a different webpage some other way.
For the above graph, there is no directed edge from node 2 to node 1.
On the Web, though, a surfer can move directly from node 2 to node 1 by entering the URL for node 1 in the address line of a web browser.
The matrix S does not consider this possibility.
|
|