Another way to measure impurity degree is using Gini index, which is a measure of statistical dispersion. It is commonly used as a measure of inequality of data.
Gini Index = 1 – Σ(pj2) for all jwhere
pj is the probability of the class value j.
For example, given that
Prob( Bus ) = 4 / 10 = 0.4 # 4B / 10 rows
Prob( Car ) = 3 / 10 = 0.3 # 3C / 10 rows
Prob( Train ) = 3 / 10 = 0.3 # 3T / 10 rows
we can now compute Gini index as
Gini index = 1 – (0.42 + 0.32 + 0.32) = 0.660Gini index of a pure table (consist of single class) is zero because the probability is 1 and
1-12=0.
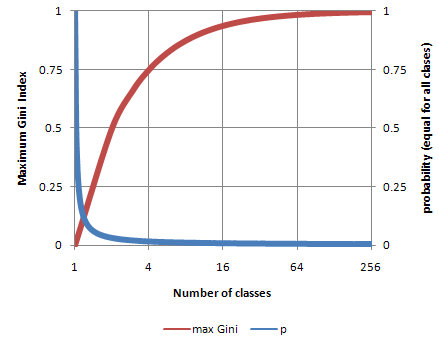
Similar to Entropy, Gini index also reaches maximum value when all classes in the table have equal probability.
The figure plots the values of maximum Gini index for different number of classes n, where probability is equal to p=1/n.
Notice that the value of Gini index is always between 0 and 1 regardless the number of classes.
|
|