An Example of Database Normalization (Cont.)

Fourth Normal Form (Cont.)
The definition of the multi-valued dependency goes as
Represent a dependency between attributes in a relation, such that for each value of A there is a set of values for B and set of values for C.
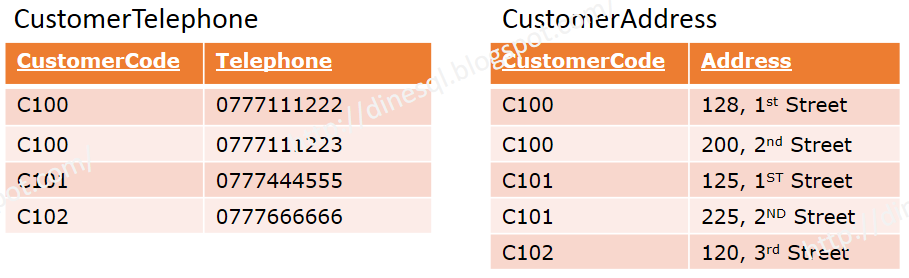
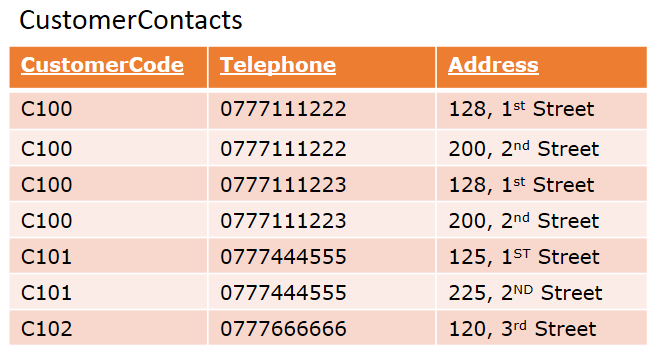
However the set of values for B and C are independent of each other. This dependency denotes as A↠B. See the CustomerContacts table.

CustomerCode determines multiple Telephone (CustomerCode ↠ Telephone) and CustomerCode determines multiple Address (CustomerCode ↠ Telephone).

The forth normal form is describes as A relation that is in Boyce-Codd normal form and does not contain nontrivial multi-valued dependencies. This talks about one type of multi-valued dependency that is nontrivial. Trivial relationship means if B is subset of A or A⋃B=R. Otherwise, it is nontrivial. As you see, CustomerContact contains nontrivial dependencies, hence need to decompose the table as below.