SQL UPDATE Statement
The UPDATE statement is used to update existing records in a table.
Notice the where clause in the update syntax.
The where clause specifies which record or records that should be updated.
If you omit the where clause, all records will be updated!
Assume the person table is given below:
|
|
UPDATE table_name
SET column1=value, column2=value2, ...
WHERE some_column=some_value;
|
|
| person_id |
last_name |
first_name |
address |
city |
| 1 |
Hansen |
Ola |
Timoteivn 10 |
Sandnes |
| 2 |
Svendson |
Tove |
Borgvn 23 |
Sandnes |
| 3 |
Pettersen |
Kari |
Storgt 20 |
Stavanger |
| 4 |
Rasmussen |
|
Storgt 67 |
|
UPDATE person SET first_name = 'Nina'
WHERE last_name = 'Rasmussen';
UPDATE person
SET address = 'Nissestien 67', city = 'Sandnes';
|
The result tables from the above two updates are shown below:
- The first update adds a first name to the person with a last name of “Rasmussen.”
|
|
| person_id |
last_name |
first_name |
address |
city |
| 1 |
Hansen |
Ola |
Timoteivn 10 |
Sandnes |
| 2 |
Svendson |
Tove |
Borgvn 23 |
Sandnes |
| 3 |
Pettersen |
Kari |
Storgt 20 |
Stavanger |
| 4 |
Rasmussen |
Nina |
Storgt 67 |
|
|
- The second update is without a where clause.
Thus, all records are updated.
|
|
| person_id |
last_name |
first_name |
address |
city |
| 1 |
Hansen |
Ola |
Nissestien 67 |
Sandnes |
| 2 |
Svendson |
Tove |
Nissestien 67 |
Sandnes |
| 3 |
Pettersen |
Kari |
Nissestien 67 |
Sandnes |
| 4 |
Rasmussen |
Nina |
Nissestien 67 |
Sandnes |
|
Demonstration
Below is an SQL test area from W3Schools, which uses the well-known Northwind sample database.
The tables here are for read only because of the problem of embedding the scripts.
For a fully working example, check this by using Chrome.
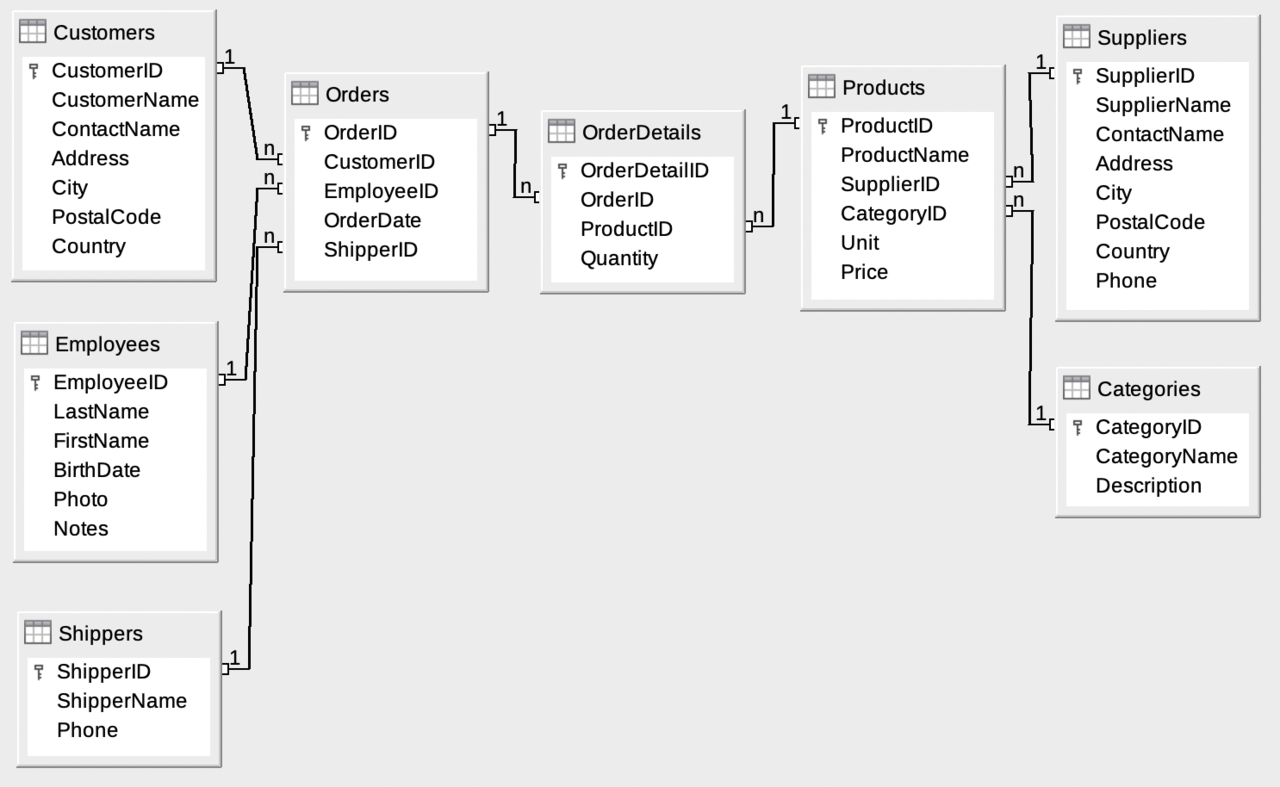
|
|
The Database includes:
| Tablename | Record |
|---|
| Customers | 91 |
| Categories | 8 |
| Employees | 10 |
| OrderDetails | 518 |
| Orders | 196 |
| Products | 77 |
| Shippers | 3 |
| Suppliers | 29 |
|
This SQL-Statement is not supported in the WebSQL Database.
The example still works, because it uses a modified version of SQL.
Your browser does not support WebSQL.
Your are now using a light-version of the Try-SQL Editor, with a read-only Database.
If you switch to a browser with WebSQL support, you can try any SQL statement, and play with the Database as much as you like. The Database can also be restored at any time.
Our Try-SQL Editor uses WebSQL to demonstrate SQL.
A Database-object is created in your browser, for testing purposes.
You can try any SQL statement, and play with the Database as much as you like. The Database can be restored at any time, simply by clicking the "Restore Database" button.
W3C WebSQL
WebSQL stores a Database locally, on the user’s computer. Each user gets their own Database object.
WebSQL Browser Support
WebSQL is supported in Chrome, Safari, and Opera.
If you use another browser you will still be able to use our Try SQL Editor, but a different version, using a server-based ASP application, with a read-only Access Database, where users are not allowed to make any changes to the data.
