A kNN Example for Extrapolation

Using the same principle of classification, we can extend the kNN algorithm for prediction (extrapolation) and smoothing (interpolation) of quantitative data (e.g., time series).

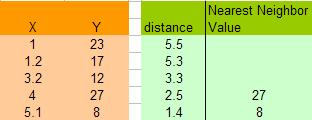
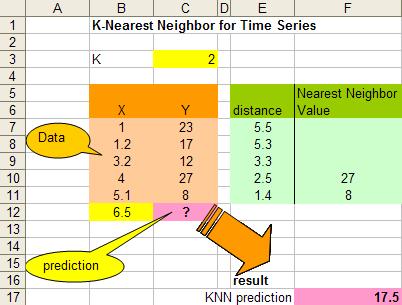
We have 5 data pair (X,Y) as shown on the right. The data are quantitative in nature. Suppose the data is sorted as in time series. Then the problem is to estimate the value of Y based on the kNN algorithm at X=6.5.
  1. Determine parameter K=number of nearest neighbors.
    Suppose use K=2.

  2. Calculate the distance between the query-instance and all the training samples.
    Coordinate of query instance is 6.5. As we are dealing with one-dimensional distance, we simply take absolute value from the query instance to value of X. For instance for X=5.1, the distance is |6.5–5.1|=1.4, for X=1.2 the distance is |6.5–1.2|=5.3 and so on.

  3. Sort the distance and determine nearest neighbors based on the Kth minimum distance.
    As the data is already sorted, the nearest neighbors are the last K data.
  1. Gather the values of Y of the nearest neighbors.
    We simply copy the Y values of the last K=2 data. The result is tabulated on the right.
  1. Use average of nearest neighbors as the prediction value of the query instance.
    In this case, we have prediction value of (27+8)/2=17.5 .