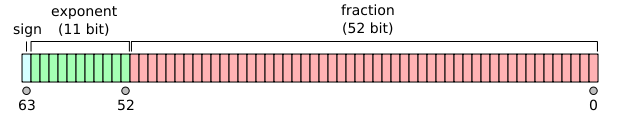
Floating-point numbers are usually a multiple of the size of a word. The representation of a MIPS floating-point number is shown below, where 1 in sign bit means negative, exponent is the value of the 8-bit exponent field (including the sign of the exponent), and fraction is the 23-bit number. The bit string represents the following number, which will be explained later:
0.15625 = (1.0+2-2)×2124-127 = 1.25×2-3

In general, floating-point numbers are of the form
(-1)S×F×2E
where F involves the value in the fraction field and E involves the value in the exponent field.
Two cases may occur for floating-point arithmetic:
- Overflow: A situation in which a positive exponent becomes too large to fit in the exponent field, and
- Underflow: A situation in which a negative exponent becomes too large to fit in the exponent field.
|
“Never forget that justice is what love looks like in public.” ― Cornel West |