- Why is it important to keep search trees balanced? (05%)
Ans>-
If a search tree is balanced, the maximum search length is minimized.
Otherwise some branches of the tree can become very long, making searches for certain items very slow.
- In what way is an AVL tree better than a simple binary search tree? (05%)
Ans>-
An AVL tree can be kept balanced with a smaller amount of overhead.
- Suppose you have a file with 4,000,000 keys stored on disk in a completely full, balanced binary search tree. (10%)
- If the tree is not paged, what is the maximum number of accesses required to find a key?
Ans>-
⌈log2(4000000+1)⌉ = 22
- If the tree is paged in the manner illustrated in Figure 9.12, but with each page able to hold 31 keys and to branch to 32 new pages, what is the maximum number of accesses required to find a key?
Ans>-
⌈log32(4000000+1)⌉ = 5
- If the page size is increased to hold 255 keys with branches to 256 nodes, how does the maximum number of accesses change?
Ans>-
⌈log256(4000000+1)⌉ = 3
- If the tree is not paged, what is the maximum number of accesses required to find a key?
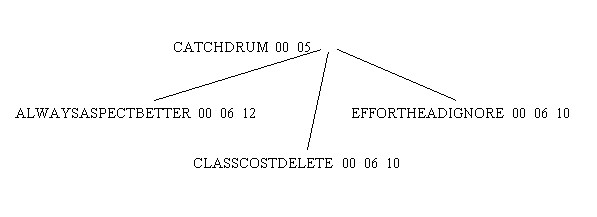
D I L M F G T Q A S N E X O K Z J B U Y
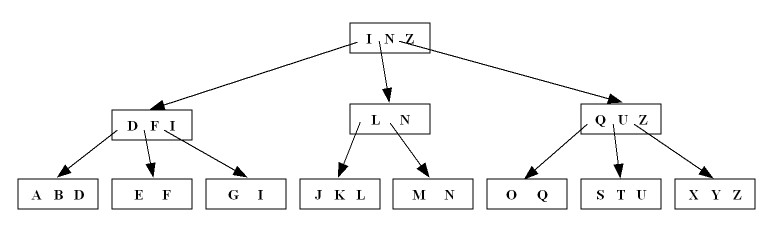
- What is the maximum number of descendants from a page?
m= 512 - What is the minimum number of descendants from a page (excluding the root and leaves)? ⌈512/2⌉ = 256
- What is the minimum number of descendants from the root? 0
- What is the maximum depth of the tree if it contains 1,000,000 keys?
Ans>-
d ≤ 1 + log ⌈512/2⌉ (1000000/2)
≤ 1 + log 256 (500000)
≤ 1 + 2.37
≤ 3.37
Therefore, the maximum depth is 3.
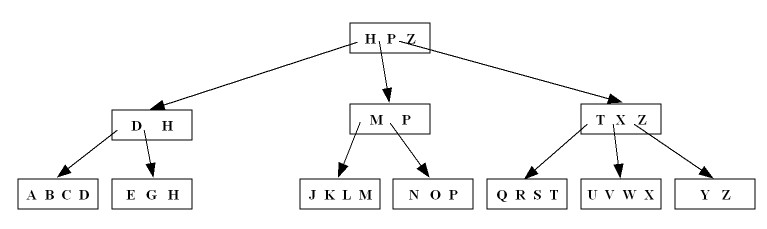
I, F, H, and G is deleted from the B-tree of Figure 9.15(c). (15%)Ans>
-
The B-tree of Figure 9.15(c):
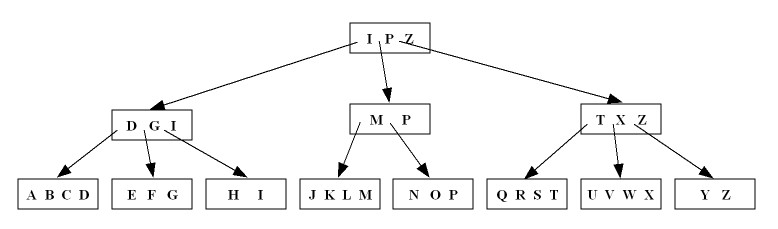
Delete the key
I and use redistribution (Rule 1.a of Slide 15.6):
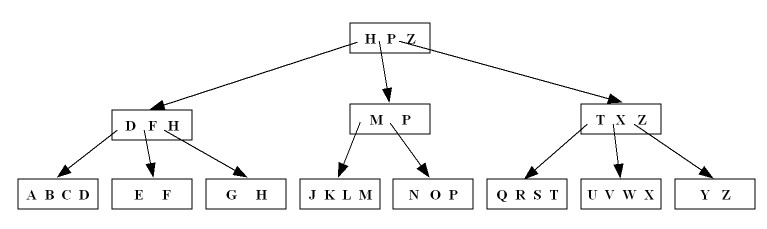
Delete the key
F and use merge (Rule 1.b of Slide 15.6):
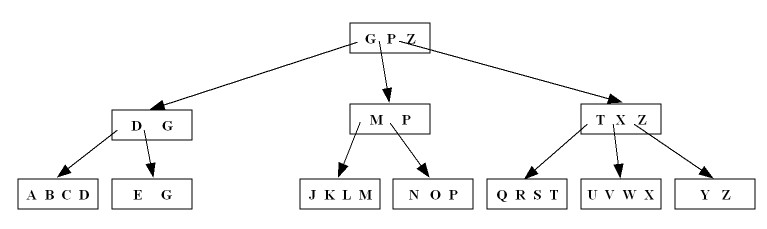
Delete the key
H:
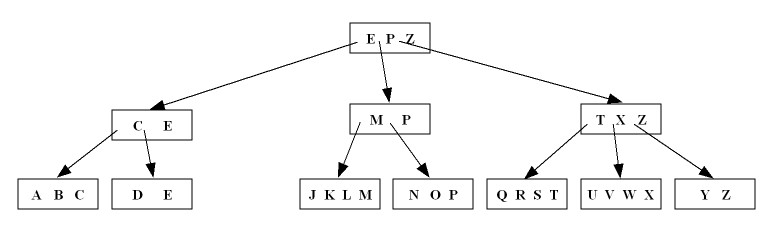
Delete the key
G and use redistribution (Rule 1.a of Slide 15.6):
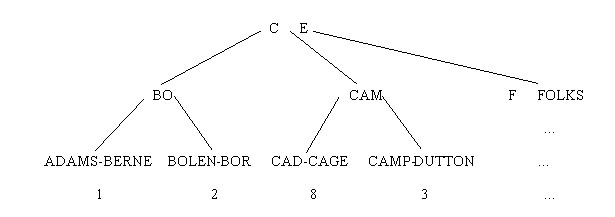
...——>Bolen—Bor——>CAD—CAGE——>... 2 8
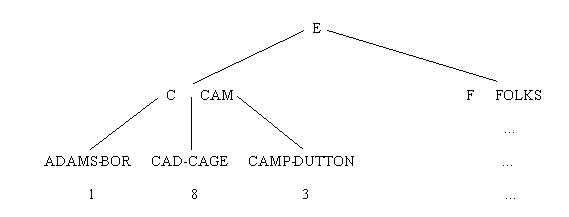
- What does the tree look like after the insertion?
Ans>-
A shortest separator must be found between Bor and CAD.
Using the scheme in the text, we choose C, which then gets inserted into the leaf node in the index set.
If we assume that the leaf node is too small to hold the three separators BO, C, and CAM, we promote C to the root.
So the tree looks like this:
- Suppose that, subsequent to the insertion, a deletion causes underflow and the consequent concatenation of Blocks 1 and 2.
What does the tree look like after the deletion?
Ans>-
After the concatenation, Block 2 is no longer needed and can be placed on an avail list.
Consequently, the separator BO is no longer needed.
Removing BO from its node in the index set forces a concatenation of index set nodes, bringing C back down from the root.
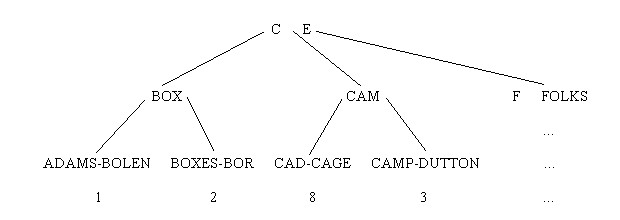
- Describe a case in which a deletion results in redistribution rather than concatenation, and show the effect it has on the tree.
Ans>-
Given the tree shown in part (a), suppose we decide to redistribute by moving the name between Nodes 2 and 1.
Suppose that the name stored after BOLEN in Node 2 is BOXES.
We move BOLEN over to the end of Node 1, then find a new separator between BOLEN and BOXES, say BOX.
BOX replaces BO in the parent.
The new tree looks like this:
Ans>
-
The sequence set remains the same, but the index set looks like this: